Below are all the questions in an actual MX2 AT1 on complex numbers, which was worth 40 marks.
I'm interested in what you think is a fair amount of time for this test (because I thought that the given time was unfair).
Question 1 (6 marks)
Consider the quadratic equationz^2 - (16 + 12i)z - 9 = 0)

Question 2 (7 marks)
Question 3 (4 marks)
Question 4 (8 marks)
Question 5 (5 marks)
Let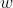 be the non-real fifth root of unity where
be the non-real fifth root of unity where 
Question 6 (5 marks)
Consider the polynomial = x^7 + 4x^4 - 3x^3 + 8x^2 - 2x + 4) over the complex numbers
over the complex numbers
Question 7 (5 marks)
Let points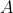 and
and 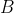 represent the complex numbers
represent the complex numbers  and
and  , respectively}
, respectively}
I note that question 1(b) shouldn't be a "hence" and would be better expressed as something like
Show that) are the solutions of
are the solutions of 
and that question 1(c) was probably meant to be "Hence, using (a) and (b), show that ..."
Also, any thoughts on the most time-efficient approach to these questions?
I'm interested in what you think is a fair amount of time for this test (because I thought that the given time was unfair).
Question 1 (6 marks)
Consider the quadratic equation
- (a) Show that the discriminant of this equation is
- (b) Hence, show that
- (c) Hence, show that the solutions of the equation are
Question 2 (7 marks)
- (a) Using De Moivre's Theorem, show that
- (b) Using part (a) and the substitution
, show that the equation
has roots
and
- (c) Hence, or otherwise, prove that
Question 3 (4 marks)
- (a) Express
in modulus-argument form
- (b) Hence, or otherwise, find the four fourth roots of
Question 4 (8 marks)
- (a) If
and
, show that
- (b) Hence, or otherwise, shade the region that satisfies both
and
- (c) If
represents Arg(
), find all possible values of
correct to 2 decimal places and represent your answer as an inequality
Question 5 (5 marks)
Let
- (a) Show that
- (b) Explain why
where
and
- (c) Using (a) and (b), show that
is a root of
Question 6 (5 marks)
Consider the polynomial
- (a) Show that
is a root of multiplicity 2, that is, is a double root
- (b) Hence, or otherwise, express
as a product of linear factors
Question 7 (5 marks)
Let points
- (a) Draw an Argand diagram that shows points
and
if
and
where
and
- (b) If
is the origin, explain why
is an equilateral triangle
- (c) Write the complex number
in exponential form in terms of
and
I note that question 1(b) shouldn't be a "hence" and would be better expressed as something like
Show that
and that question 1(c) was probably meant to be "Hence, using (a) and (b), show that ..."
Also, any thoughts on the most time-efficient approach to these questions?
